エンでエンエンエン

スタンダードミニ

もしもピアノが弾けたなら

なんとエンでエンエンエンでは非常に珍しい、連載ものである。テイラー展開をそのまましつこくつづけていたんだぁあたくしや。

早速だがいろいろ試していた楽しい時間は終わりで、Cでテイラー展開の式をコピった。こういう式を実装するときに、いろいろな難問が私たちにはおしよせる。

「早く結果が見たい」

だとか

「それよりスマートな物が書きたい」

だとか

「効率的なものがほしい」

とか

「納期回答は」「当社の勝ちパターンです」「よっし、新プロジェクトのはたあげだー」（メガネ親父力説）

とかとか

とかくこの世は勘定奉行である。しかしそういう迷いは長机（いすじゃなくて）に足をひっかけて、帽子をあげ「あんたの実装は確かに早い、だが、世界で二番目だ」そうすると大阪ボスが「じゃあ、一番はだれだ」そこで指を自分に向けて（オレ）これでメンタルな部分はすべて解決する。

こういう気持ちがおしよせてきたときには、まずがまんをするというのが肝心だ。あせってもいけない、しかし遅れてもいけない、遅れるぎりぎりのところで差し出す。とかもいってらんないのでまず結果。結果が肝心。

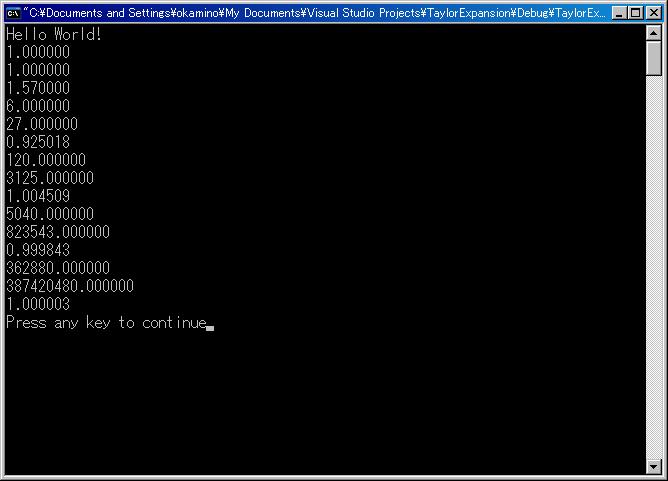
これだけだと何やってんだかゼンゼンわかんないなさすがに、他人用に注をつけよう。

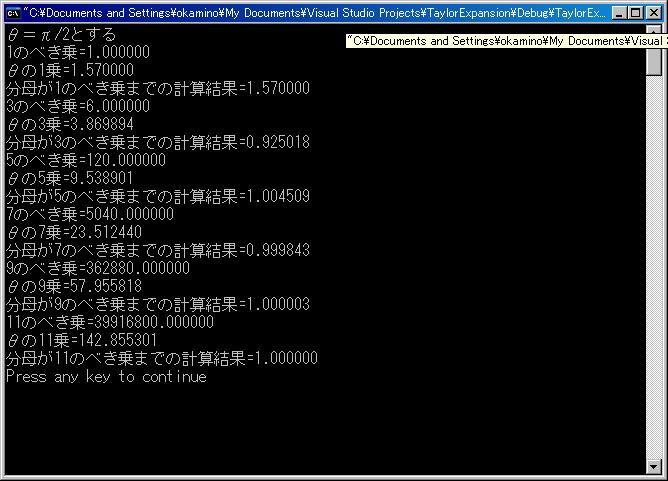
ということで、π/2のサインを出すのにだいたい９乗から信用に足る結果が出ることがわかった。

アセンブルのにC言語の命令だとちょっと便利度が高いので、アセンブる用にソースを再検討することにする。

まず桁あふれの問題があろう、もし１１桁までの実装だと大きいほうで８桁の計算ができないといけない。

さらに小数点の桁数と精度の問題があり、現在小数点第６位まで計算しているがそこまで結果が必要かわかならい。今回の目的は２５６＊２５６ドットぐらいの四角形の中に入る円を書きたいだけなので、シリコダマのつやまでわかるような微細な精度は求められていない。どのぐらいの計算までやればいいのかによってもかなり作業がらくになっていくと思うので、ここは一つまわりみちして、どんぐらいの精度でどんぐらいの円が書けるかについてかんがえてみたい。エンエンエーン

とりあえずは先ほどの結果を組み入れることにした

なんじゃこりゃ、円じゃないじゃん。ブー。

こんなところでくじけている場合でもないので、このまますすめていく。

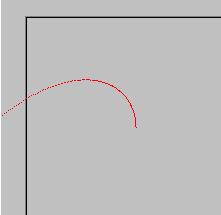
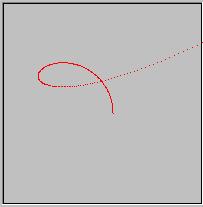
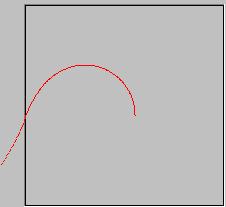
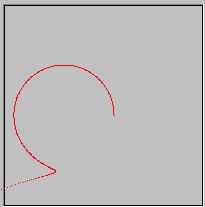
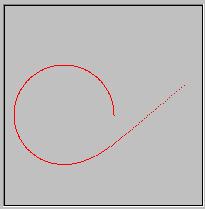
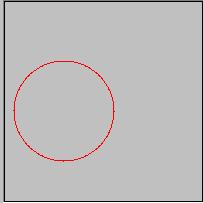
ということで、夏休みのあさがおの成長か、がんばれベアーズのエラーシーンかというぐらいになってしまったが。

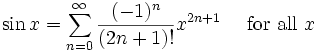
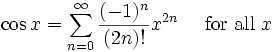
の無限大は無理なのでnの数を９まであげてみた結果がこれだ。乗数をあげていけば円もきれいになっていくのが分かるかと思う。

先ほどの検算プログラムに９まで入れて桁数を調べてみる。

θ＝π/2とする

1のべき乗=1.000000:θの1乗=1.570000

分母が1のべき乗までの計算結果=1.570000

3のべき乗=1.000000:θの3乗=1.570000

分母が3のべき乗までの計算結果=0.925018

5のべき乗=2.000000:θの5乗=2.464900

分母が5のべき乗までの計算結果=1.004509

7のべき乗=6.000000:θの7乗=3.869894

分母が7のべき乗までの計算結果=0.999843

9のべき乗=24.000000:θの9乗=6.075733

分母が9のべき乗までの計算結果=1.000003

11のべき乗=120.000000:θの11乗=9.538901

分母が11のべき乗までの計算結果=1.000000

13のべき乗=720.000000:θの13乗=14.976075

分母が13のべき乗までの計算結果=1.000000

15のべき乗=5040.000000:θの15乗=23.512440

分母が15のべき乗までの計算結果=1.000000

17のべき乗=40320.000000:θの17乗=36.914532

分母が17のべき乗までの計算結果=1.000000

19のべき乗=362880.000000:θの19乗=57.955818

分母が19のべき乗までの計算結果=1.000000

21のべき乗=3628800.000000:θの21乗=90.990639

分母が21のべき乗までの計算結果=1.000000

23のべき乗=39916800.000000:θの23乗=142.855301

分母が23のべき乗までの計算結果=1.000000

５０の直径の円を書くのに、べき乗で８桁、乗数で９桁の桁が必要なようだ。ここでもオレはあの聳え立つたかいやまのことを思い出す。そして考えるのだ「どうしよう」と。

たとえば３のべき乗までの計算でも90度までなら計算結果は間違いなく出てるみたいだから、これを鏡のように展開していけば望みの結果がでるのではないだろうか。これは志村けんのだいじょうぶだぁでも実証済みだ。

　→　　→　 こんな感じ、だいじょうぶだあ。

モデルはだいじょうぶだあに出演していた人

そうすれば基本的に３桁の数の割り算で計算がすむかもしれない。しかし、実際のところラディアンを出すのにπ/180としているので、そこの小数点も心配だし。割り算の結果で出るサインの結果も心配だ。結局少数第何位までつかってあの円が出ているのかもう少し調べないと時間やコードの節約になるのかあやしいもんだ。どうすればいいんだ、どうすれば

サナギマーーーン　　チェイン具　つづく